Factoring quadratic trinomials can be a big speed bump in Algebra.
Click here to view a brief recording of a method I developed that helps the student to visualize the process.
I call this the X-Method.
You can find a written lesson below.
Click here to view a brief recording of a method I developed that helps the student to visualize the process.
I call this the X-Method.
You can find a written lesson below.
Factoring Quadratic Trinomials (No leading coefficient)
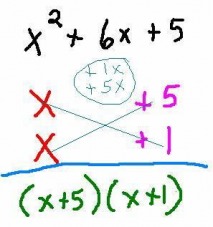
Begin by writing the trinomial in descending order of exponents.
Look at the first term. On the 2 lines directly below it write its only possible factors 'x' and 'x'.
Look at the last term. Notice that it is prime and its only possible factors are '1' and '5'. Write these below the 5.
Check your work by multiplying DIAGONALLY and writing your answers (small) below the middle term. If these answers add up to be the middle term your factoring is correct. Circle the (small) terms to get them out of the way.
Draw a line under your work for clarity.
Write the binomial on the second line multiplied by the binomial on the third line as your final answer.
Now lets relate what we just did back to the FOIL method of multiplying binomials:
The red factors are your First terms
The dark green (small) factors are your Inner and Outer terms
The purple factors are your Last terms
Look at the first term. On the 2 lines directly below it write its only possible factors 'x' and 'x'.
Look at the last term. Notice that it is prime and its only possible factors are '1' and '5'. Write these below the 5.
Check your work by multiplying DIAGONALLY and writing your answers (small) below the middle term. If these answers add up to be the middle term your factoring is correct. Circle the (small) terms to get them out of the way.
Draw a line under your work for clarity.
Write the binomial on the second line multiplied by the binomial on the third line as your final answer.
Now lets relate what we just did back to the FOIL method of multiplying binomials:
The red factors are your First terms
The dark green (small) factors are your Inner and Outer terms
The purple factors are your Last terms
Factoring Quadratic Trinomials (leading coefficient)

In this example the first term has a coefficient of '8' and a squared term. First factor the squared term as 'x' and 'x'.. The last term is prime so it is easier to begin by writing the factors of 3 (purple). Now we can mentally 'play' with the possible factors of '8' (which are 1 and 8 or 2 and 4) so that when we multiply the DIAGONALS (dark green) we get the middle term when we add the parts together (small circled numbers). Notice that the largest 'cross product' will have the same sign as the middle term.
Factoring Quadratic Trinomials (leading coefficient AND composite last term)
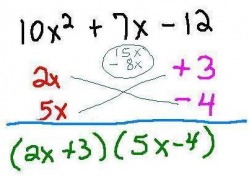
In this example we face multiple problem areas. We have a leading coefficient AND the last term is composite--not to mention that the last term is also negative. Because the last term is negative I know that one of the factors will be negative and the other positive. Instead of 3 possible factor combinations we now have 6--just for the last term!
(1 and -12, -1 and 12 -2 and 6, 2 and -6 -3 and 4, 3 and -4)
In this case it does not matter which side you begin on... I tried the 'middle' factors of 10 combined with the 'middle' factors of 12. When I tried a positive 4 on the fist line the result was -6x +20x=14x (too much). I then tried a negative 4 and the result was -20x +6x=-14x (not enough)... finally I tried a positive 3 on top and it worked! It takes a bit of practice to learn how to do these mentally--I tend to always do mine on scrap paper.
Remember this method is still 'guess and check'... but for some reason writing it out in this form where you can easily see the diagonal multiplication is usually easier--plus it is SELF-CHECKING!
(1 and -12, -1 and 12 -2 and 6, 2 and -6 -3 and 4, 3 and -4)
In this case it does not matter which side you begin on... I tried the 'middle' factors of 10 combined with the 'middle' factors of 12. When I tried a positive 4 on the fist line the result was -6x +20x=14x (too much). I then tried a negative 4 and the result was -20x +6x=-14x (not enough)... finally I tried a positive 3 on top and it worked! It takes a bit of practice to learn how to do these mentally--I tend to always do mine on scrap paper.
Remember this method is still 'guess and check'... but for some reason writing it out in this form where you can easily see the diagonal multiplication is usually easier--plus it is SELF-CHECKING!
Additional Examples
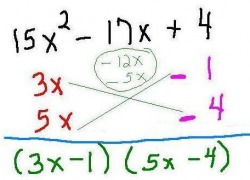
In this example the middle term is NEGATIVE and the last term is POSITIVE. For this to work the factors of the last term must BOTH be NEGATIVE.
Special Case Quadratics
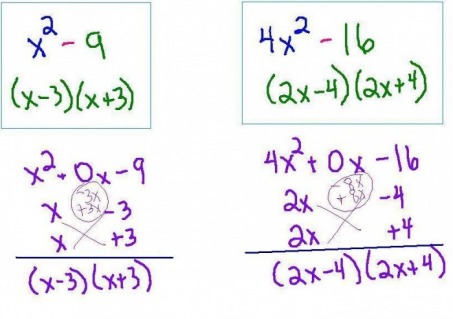
The pattern of these examples is often called 'The Difference of Two Squares'. Notice that both terms are perfect squares. Eventually it will become easy to remember the pattern (the two roots added multiplied by the two roots subtracted)--but if you ever need to you can fill in the missing 'middle term' with a '0' and factor using the above methods.
